01. Matrix

---

Given an m x n binary matrix mat, return the distance of the nearest 0 for each cell.

The distance between two adjacent cells is 1.

 

Example 1:

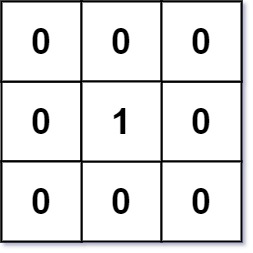
Input: mat = [[0,0,0],[0,1,0],[0,0,0]]
Output: [[0,0,0],[0,1,0],[0,0,0]]

Example 2:

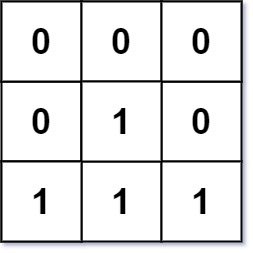
Input: mat = [[0,0,0],[0,1,0],[1,1,1]]
Output: [[0,0,0],[0,1,0],[1,2,1]]

 

Constraints:

• m == mat.length
• n == mat[i].length
• 1 <= m, n <= 104
• 1 <= m * n <= 104
• mat[i][j] is either 0 or 1.
• There is at least one 0 in mat.

 class Solution:
    def updateMatrix(self, matrix: List[List[int]]) -> List[List[int]]:
        from collections import deque
        visited = set()
        q = deque()

        ROW = len(matrix)
        COL = len(matrix[0])

        combinations = [
            [-1,0],
            [0,-1],
            [0, 1],
            [1, 0]
        ]

        for i in range(ROW):
            for j in range(COL):
                if matrix[i][j] == 0:
                    q.append([i, j])
                    visited.add((i, j))

        while q:
            x, y = q.popleft()
            for dirr in combinations:
                newX, newY = x+ dirr[0], y+ dirr[1]
                if newX < ROW and newX >=0 and newY < COL and newY >= 0 and (newX, newY) not in visited:
                    matrix[newX][newY] = matrix[x][y] + 1
                    q.append([newX, newY])
                    visited.add((newX, newY))

        return matrix