94. Binary Tree Inorder Traversal

Given the root of a binary tree, return the inorder traversal of its nodes' values.

Example 1:

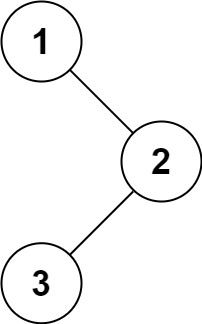
Input: root = [1,null,2,3]
Output: [1,3,2]

Example 2:

Input: root = []
Output: []

Example 3:

Input: root = [1]
Output: [1]

Constraints:

The number of nodes in the tree is in the range [0, 100].
-100 <= Node.val <= 100

Follow up: Recursive solution is trivial, could you do it iteratively?

SolvingApproachs:

Approach 1: Recursive Approach

The first method to solve this problem is using recursion. This is the classical method and is straightforward. We can define a helper function to implement recursion.

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        helper(root, res);
        return res;
    }

    public void helper(TreeNode root, List<Integer> res) {
        if (root != null) {
            helper(root.left, res);
            res.add(root.val);
            helper(root.right, res);
        }
    }
}

Complexity Analysis

Time complexity: $O(n)$

The time complexity is $O(n)$ because the recursive function is $T(n) = 2 \cdot T(n/2)+1$ .

Space complexity: $O(n)$

The worst case space required is $O(n)$ , and in the average case it's $O(\log n)$ where $n$ is number of nodes.

Approach 2: Iterating method using Stack

The strategy is very similiar to the first method, the different is using stack.

public class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        Stack<TreeNode> stack = new Stack<>();
        TreeNode curr = root;
        while (curr != null || !stack.isEmpty()) {
            while (curr != null) {
                stack.push(curr);
                curr = curr.left;
            }
            curr = stack.pop();
            res.add(curr.val);
            curr = curr.right;
        }
        return res;
    }
}

Complexity Analysis

Time complexity: $O(n)$

Space complexity: $O(n)$

Approach 3: Morris Traversal

In this method, we have to use a new data structure-Threaded Binary Tree, and the strategy is as follows:

Step 1: Initialize current as root

Step 2: While current is not NULL,

If current does not have left child

    a. Add current’s value

    b. Go to the right, i.e., current = current.right

Else

    a. In current's left subtree, make current the right child of the rightmost node

    b. Go to this left child, i.e., current = current.left

For example:

First, 1 is the root, so initialize 1 as current, 1 has left child which is 2, the current's left subtree is

         2
        / \
       4   5

So in this subtree, the rightmost node is 5, then make the current(1) as the right child of 5. Set current = cuurent.left (current = 2). The tree now looks like:

For current 2, which has left child 4, we can continue with thesame process as we did above

then add 4 because it has no left child, then add 2, 5, 1, 3 one by one, for node 3 which has left child 6, do the same as above. Finally, the inorder taversal is [4,2,5,1,6,3].

For more details, please check Threaded binary tree and Explaination of Morris Method

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        TreeNode curr = root;
        TreeNode pre;
        while (curr != null) {
            if (curr.left == null) {
                res.add(curr.val);
                curr = curr.right; // move to next right node
            } else { // has a left subtree
                pre = curr.left;
                while (pre.right != null) { // find rightmost
                    pre = pre.right;
                }
                pre.right = curr; // put cur after the pre node
                TreeNode temp = curr; // store cur node
                curr = curr.left; // move cur to the top of the new tree
                temp.left = null; // original cur left be null, avoid infinite loops
            }
        }
        return res;
    }
}

Complexity Analysis

Time complexity: $O(n)$

To prove that the time complexity is $O(n)$ , the biggest problem lies in finding the time complexity of finding the predecessor nodes of all the nodes in the binary tree. Intuitively, the complexity is $O(n \log n)$ , because to find the predecessor node for a single node related to the height of the tree. But in fact, finding the predecessor nodes for all nodes only needs $O(n)$ time. Because a binary Tree with $n$ nodes has $n-1$ edges, the whole processing for each edges up to 2 times, one is to locate a node, and the other is to find the predecessor node. So the complexity is $O(n)$ .

Space complexity: $O(1)$

Extra space is only allocated for the ArrayList of size $n$ , however the output does not count towards the space complexity.

Recursive way

def inorderTraversal(self, root):
        """ Inorder Tree traversal with recursive function call.  left -> root -> right """
        if root:
            self.inorderTraversal(root.left)
            #print(root.val)
            self.result.append(root.val)
            self.inorderTraversal(root.right)

        return self.result

Iterative way

def inorder_traversal_iterative(self, root):
        """ Using Iterative method to traverse tree in in-order manner."""
        current = root
        stack = []

        while current or stack:
            while current:
                stack.append(current)
                current = current.left

            # list.pop() has default -1, which is the last element (recent)
            current = stack.pop()
            self.result.append(current.val)
            current = current.right

        return self.result

94. Binary Tree Inorder Traversal

Approach 1: Recursive Approach

Approach 2: Iterating method using Stack

Approach 3: Morris Traversal

Related

Random Note