160. Intersection Of Two Linked Lists

Easy

Given the heads of two singly linked-lists headA and headB, return the node at which the two lists intersect. If the two linked lists have no intersection at all, return null.

For example, the following two linked lists begin to intersect at node c1:

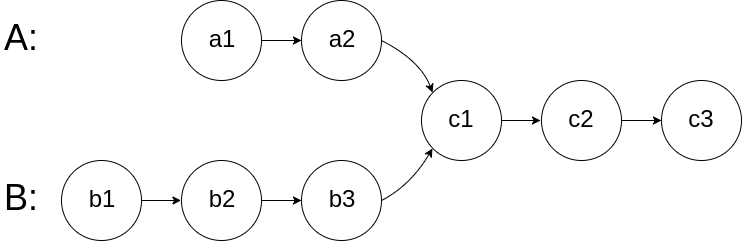
The test cases are generated such that there are no cycles anywhere in the entire linked structure.

Note that the linked lists must retain their original structure after the function returns.

Custom Judge:

The inputs to the judge are given as follows (your program is not given these inputs):

intersectVal - The value of the node where the intersection occurs. This is 0 if there is no intersected node.
listA - The first linked list.
listB - The second linked list.
skipA - The number of nodes to skip ahead in listA (starting from the head) to get to the intersected node.
skipB - The number of nodes to skip ahead in listB (starting from the head) to get to the intersected node.

The judge will then create the linked structure based on these inputs and pass the two heads, headA and headB to your program. If you correctly return the intersected node, then your solution will be accepted.

Example 1:

Input: intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA = 2, skipB = 3
Output: Intersected at '8'
Explanation: The intersected node's value is 8 (note that this must not be 0 if the two lists intersect).
From the head of A, it reads as [4,1,8,4,5]. From the head of B, it reads as [5,6,1,8,4,5]. There are 2 nodes before the intersected node in A; There are 3 nodes before the intersected node in B.

Example 2:

Input: intersectVal = 2, listA = [1,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
Output: Intersected at '2'
Explanation: The intersected node's value is 2 (note that this must not be 0 if the two lists intersect).
From the head of A, it reads as [1,9,1,2,4]. From the head of B, it reads as [3,2,4]. There are 3 nodes before the intersected node in A; There are 1 node before the intersected node in B.

Example 3:

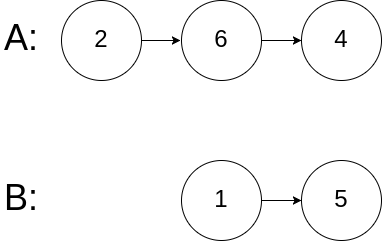
Input: intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
Output: No intersection
Explanation: From the head of A, it reads as [2,6,4]. From the head of B, it reads as [1,5]. Since the two lists do not intersect, intersectVal must be 0, while skipA and skipB can be arbitrary values.
Explanation: The two lists do not intersect, so return null.

Constraints:

The number of nodes of listA is in the m.
The number of nodes of listB is in the n.
1 <= m, n <= 3 * 10⁴
1 <= Node.val <= 10⁵
0 <= skipA < m
0 <= skipB < n
intersectVal is 0 if listA and listB do not intersect.
intersectVal == listA[skipA] == listB[skipB] if listA and listB intersect.

Follow up: Could you write a solution that runs in O(m + n) time and use only O(1) memory?

 # Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    def getIntersectionNode(self, headA: ListNode, headB: ListNode) -> Optional[ListNode]:
        # hashset = set()
        # nodeA = headA
        # nodeB = headB

        # while nodeA or nodeB:

        #     if nodeA is not None:
        #         if nodeA in hashset:
        #             return nodeA
        #         hashset.add(nodeA)

        #     if nodeB is not None:
        #         if nodeB in hashset:
        #             return nodeB
        #         hashset.add(nodeB)

        #     if nodeA is not None:
        #         nodeA = nodeA.next
        #     if nodeB is not None:
        #         nodeB = nodeB.next

        # return None

        # hashset =set()
        # node = headA
        # while node:
        #     hashset.add(node)
        #     node = node.next

        # node = headB
        # while node:
        #     if node in hashset:
        #         return node
        #     node = node.next
        # return None

        # with two pointer technique
        # method:
        # if la == lb, no problem, we'll just get it
        # different: d = abs(a-b), when one pointer  hit null, and the other p2 position, then if we point the short pointer to the head of longer node
        # that will be ahead of the longer node with d distance
        # then when the longer node pointer hit null, we'll point to the shorter head, at this time our short pointer is alredy passed d distance
        # which is the difference;
        # now the will move keeping the pace, and intersect with their meeting point.


        nodeA = headA
        nodeB = headB

        while nodeA != nodeB:
            nodeA = headB if nodeA is None else nodeA.next
            nodeB = headA if nodeB is None else nodeB.next

        return nodeA

160. Intersection Of Two Linked Lists

Random Note